Monomial order

In mathematics, a monomial order is a total order on the set of all (monic) monomials in a given polynomial ring, satisfying the following two properties:

If u < v and w is any other monomial, then uw<vw. In other words, the ordering respects multiplication.
The ordering is a well ordering (every non-empty set of monomials has a minimal element).

Among the powers of any one variable x, the only ordering satisfying these conditions is the natural ordering 1<x<x²<x³... (with only the first condition, the opposite ordering would also qualify, but the set of all powers of x would fail to have a minimal element). Therefore the notion of monomial ordering is interesting only in the case of multiple variables.

Monomial orderings are most commonly used with Gröbner bases and multivariate division.

Examples of monomial orders

The monomial order implies an order on the individual indeterminates. One can simplify the classification of monomial orders by assuming that the indeterminates are named x₁, x₂, x₃, ... in decreasing order for the monomial order considered, so that always x₁ > x₂ > x₃ > …. (If there should be infinitely many indeterminates, this convention is incompatible with the condition of being a well ordering, and one would be forced to use the opposite ordering; however the case of polynomials in infinitely many variables is rarely considered.) In the example below we shall use x instead of x₁, y instead of x₂, and z instead of x₃. With this convention there are still many examples of different monomial orders.

Lexicographic order (lex). This ordering first compares exponents of x₁ in the monomials, and in case of equality compares exponents of x₂, and so forth. The name is derived from the similarity with the usual lexicographic order on words, if monomials are represented by the sequence of the exponents of the indeterminates. The failure of dictionary order to be a well ordering does not present a problem here when there are finitely many indeterminates, because all sequences have the same length. For Gröbner basis computations this ordering uses to be the most costly; thus it should be avoided, as far as possible, unless for very simple computations.

Graded lexicographic order (grlex). This ordering first compares the total degree (sum of all exponents), and in case of a tie applies lexicographic order. This ordering is not only a well ordering, it also has the property that any monomial is preceded only by a finite number of other monomials; this is not the case for lexicographic order, where all (infinitely many) powers of y are less than x (that lexicographic order is nevertheless a well ordering is related to the impossibility to construct an infinite decreasing chain of monomials). Although very natural, this ordering is rarely used: the Gröbner basis for the graded reverse lexicographic order, which follows, is easier to compute and provides the same information on the input set of polynomials.

Graded reverse lexicographic order (grevlex) compares the total degree first, then compares exponents of the last indeterminate x_n but reversing the outcome (so the monomial with smaller exponent is larger in the ordering), followed (as always only in case of a tie) by a similar comparison of x_n−1, and so forth ending with x₁. The reversal of the outcome is necessary to get the conventional ordering x₁ > x₂ > x₃ > … of the indeterminates. Unlike for graded lexicographic order, the ungraded version of this ordering does not give a monomial ordering, since the (increasing) powers of any single indeterminate would form an infinite decreasing chain. Indeed, thanks to the comparison of total degree first, the reversal of subsequent comparisons can be interpreted informally as follows: the monomial with a smaller power of x_n necessarily has a higher power of some (unspecified) x_i with i<n (indeed it has greater total degree with respect to all indeterminates other than x_n).

Block or elimination order (lexdeg). This kind of ordering may be defined for any number of blocks but, for sake of simplicity, we consider only the case of two blocks (however, if the number of blocks equals the number of variables, this order is simply the lexicographic order). For this ordering, the variables are divided in two blocks x₁,..., x_h and y₁,...,y_k and a monomial ordering is chosen for each block, usually the graded reverse lexicographical order. Two monomials are compared by comparing their x part, and in case of a tie, by comparing their y part. This ordering is important as it allows elimination an operation which corresponds to projection in algebraic geometry.

A weight orders depends on a sequence 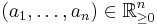$(a_1,\ldots,a_n)\in\R_{\geq0}^n$ called the weight vector. It first compares the dot product of the exponent sequences of the monomials with this weight vector, and in case of a tie uses some other fixed monomial order. For instance, the graded orders above are weight orders for the "total degree" weight vector (1,1,...,1). If the a_i are rationally independent numbers (so in particular none of them are zero and all fractions 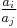$\tfrac{a_i}{a_j}$ are irrational) then a tie can never occur, and the weight vector itself specifies a monomial ordering. In the contrary case, one could use another weight vector to break ties, and so on; after using n linearly independent weight vectors, there cannot be any remaining ties. One can in fact define any monomial ordering by a sequence of weight vectors (Cox et al. pp. 72-73), for instance (1,0,0,...,0), (0,1,0,...,0), ... (0,0,...,1) for lex, or (1,1,1,...,1), (1,1,...,,1,0), ... (1,0,...,0) for grevlex.

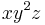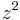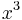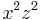For example, consider the monomials $xy^2z$ , $z^2$ , $x^3$ , and $x^2z^2$ ; the monomial orders above would order these four monomials as follows:

Lex: 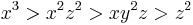$x^3 > x^2z^2 > xy^2z > z^2$ (power of $x$ dominates).
Grlex: 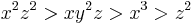$x^2z^2 > xy^2z > x^3 > z^2$ (total degree dominates; higher power of $x$ broke tie among the first two).
Grevlex: 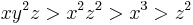$xy^2z > x^2z^2 > x^3 > z^2$ (total degree dominates; lower power of $z$ broke tie among the first two).
A weight order with weight vector (1,2,4): 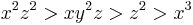$x^2z^2 > xy^2z > z^2 > x^3$ (the dot products 10>9>8>3 do not leave any ties to be broken here).

Some notions related to monomial orders

An elimination order guarantees that a monomial involving any of a set of indeterminates will always be greater than a monomial not involving any of them.

A product order is the easier example of an elimination order. It consists in combining monomial orders on disjoint sets of indetermines into a monomial order on their union. It simply compares the exponents of the indeterminates in the first set using the first monomial order, then breaks ties using the other monomial ordering on the indeterminates of the second set. This method obviously generalizes to any disjoint union of sets of intertermines; the lexicographic order can be so obtained from the singleton sets {x₁}, {x₂}, {x₃}, ... (with the unique monomial ordering for each singleton).

When using monomial orderings to define Gröbner bases, different orders can lead to different results. For example, graded reverse lexicographic order has a reputation for producing relatively small Gröbner bases, while elimination orders can be used with the same algorithms to solve systems of polynomial equations by eliminating variables.

References

David Cox; John Little; Donal O'Shea (2007). Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra. Springer. ISBN 0-387-35650-9.